期中考试困难MySQL总结
知识点
- ALL SOME(ANY)
NULL带来的干扰 -> 将TF变成三值逻辑:
- 有NULL值会影响ALL,如where gdp > all(select gdp from world where continent = 'Europe'),由于部分gdp为NULL,where gdp > NULL将不会成立。
- 有NULL值会影响NOT IN,如WHERE Sdept NOT IN (‘CS’,’MA’,’IS’);当Sdept为NULL时整条语句为unknown状态,正确的是:WHERE Sdept NOT IN (‘CS’,’MA’,’IS’) IS NOT FALSE; 这样可以选中不属于这三个、但是为NULL的元组
- 多表连接查询: join默认是inner join(等值连接)与", + where"类似;left/right outer join为左右外连接;
- 带有EXISTS的子查询√ 注意看双重否定,如“至少选修A老师所授全部课程”->“没有一门A老师的课是学生x没有选的”
- group by having: having是限制选出的组的条件,而不是限制元组的条件,限制元组的条件用where。
- with A as (XXX) 将XXX执行结果临时作为A
借了所有A作者出版的书的读者:(查询成员x,A出的书没有不在他的借书列表的?)
- 两个not exists 或者not exists + except
select distinct name from member m where not exists(
select * from book bo where author = 'A' and not exists(
select * from borrowed b where bo.isbn = b.isbn and m.name = b.name
)
)
select distinct name from member m where not exists(
(select isbn from book bo where author = 'A') except (select isbn from borrowed b where bo.isbn = b.isbn and m.name = b.name)
)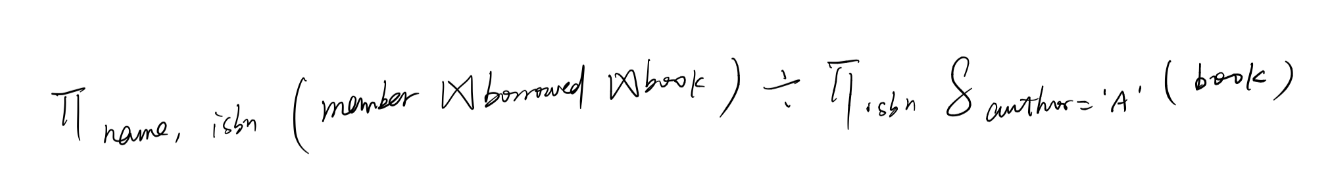
内外关联查询
在每一個州中找出最大面積的國家,列出洲份 continent, 國家名字 name 及面積 area。
select continent, name, area from world x where area >= all( select area from world y where y.continent = x.continent and area > 0 )
insert、update、delete、create table、create index:
- insert into table(f1, f2, ...) values (v1, v2, ...);
- update table set x = 0.1*x where...
- delete from table where ...
- create table student(Sno CHAR(9) PRIMARY KEY, Sname CHAR(20) UNIQUE,... PRIMARY KEY(Sno, Cno), FOREIGN KEY (Sno) REFERENCE Student(Sno) )
例题
- 找出工资高于A公司的每个雇员的所有雇员;(每个用>ALL, 或者>MAX,属于最大值问题)
- 至少选修A老师所授全部课程(同借了所有A作者出版的书的读者,)
关系代数
- 选择
- 投影:(在移除不需要的属性的同时,还会移除因此导致的重复的行)
- 连接:普通连接、等值连接(内连接)、左右外连接、自身连接
除法:
- 划分两个关系的XYZ:其中Y是相同域集的属性集(一般同名)
- 为X的每一种属性组合定义其象集:如a3的象集是{(b4, c6), (b2,c1)};
- R$\div$S的结果为:X中那些 象集包含了 “S在Y属性集上投影“ 的所有属性组合的集合
- 可以发现,除法运算与Z无关
- 下面的R$\div$S为{a3},因为a3的象集包含了S在B、C上的投影
| A(X) | B(Y) | C(Y) |
| a1 | b1 | c2 |
|---|---|---|
| a2 | b3 | c7 |
| a3 | b4 | c6 |
| ... | ... | ... |
| a3 | b2 | c1 |
| B(Y) | C(Y) | D(Z) |
| ---- | ---- | ---- |
| b4 | c6 | d1 |
E-R图构建 & E-R到关系模型(结合第一章、第六章)
构建
- 带箭头的联系 $\rightarrow$ 箭头端是1
- 双线联系是全参与(total participation):实体集中所有实体都出现在联系中,与之对应的部分参与可以允许部分实体不出现在联系中;
- 双线方框是弱实体集(所有属性都无法构成主码,无法唯一确定元组),弱实体集的联系都是弱联系(双线菱形),都是一对多的联系,弱实体参与联系时应该是“完全参与”(画在N端);弱实体集的主码由自身的分辨符(discriminating key)+强实体集的主码构成;
E-R到关系模型
- 1:1关系:在任一实体中添加另一实体的主键;
- 1:N关系:在N端添加另一端的主键,如老师与学生是一对多关系,只需要在学生端加上老师的主键;
- M:N关系:需要将联系转换为实体,并在此实体上加上两端主键;如选课关系是学生与课程的多对多关系,新建SC关系,并将学生主键Sno和课程主键Cno添加进来;
- 1:1:N关系:在N端添加另外两端的主键
- M:N:P关系:新建实体,添加三端主键(同多对多关系的转换)
范式判断
函数依赖
$ X \rightarrow Y$:X函数确定Y;Y函数依赖于X,语义为X一旦确定,Y也随即确定;
如果$ Y \subsetneq X$,那$X\rightarrow Y$还是非平凡的函数依赖;(如果Y是X的子集,函数依赖关系是显然的,所以是平凡的)
$X\stackrel{F}{\rightarrow}Y$:Y对X完全函数依赖(对任何X',$X' \stackrel{F}\rightarrow Y$不再成立,即X是使函数依赖成立的最小的属性集。)
$X\stackrel{P}{\rightarrow}Y$:Y对X部分函数依赖(与完全函数依赖相对)
$X\stackrel{传递}{\rightarrow}Z$:可以由两个非平凡的$X\rightarrow Y$,$Y\rightarrow Z$得来
函数依赖意义下的候选码
$K\stackrel{F}{\rightarrow}U$:对R<U,F>,有此式成立,K就是R的候选码;(候选码可以函数确定其他所有属性)
其余含义与之前保持一致,包括:
- 主码:候选码中的选定的一个;
- 主属性:任何包含在候选码中的属性;
- 非主属性:U-主属性;
- 全码:整个属性组都是码;
- 1NF:符合1NF的关系中的每个属性都不可再分;
2NF:(等价说法)
- 对所有非平凡的函数依赖$X\rightarrow Y$,要么Y为主属性,要么X不是任何码(候选码)的真子集;
- 不存在非主属性对码的部分函数依赖;(不存在$候选码 \stackrel{P}\rightarrow 非主属性$)
3NF:
- 对所有非平凡的函数依赖$X\rightarrow Y$,要么Y为主属性,要么X包含码;(X包含码,X就不会是码的真子集,所以3NF一定是2NF)
- 不存在非主属性对码的传递函数依赖;(不存在$候选码 \stackrel{传递}\rightarrow 非主属性$)
BCNF:
- 对所有非平凡的函数依赖$X\rightarrow Y$,X包含码;
- 不存在主属性对码的部分函数依赖和传递函数依赖;
- BCNF将不存在由于过度冗余导致的三大异常(修改复杂、插入异常、删除异常)
- trick:全码一定是BCNF;
多值依赖
对给定的R(U),$X\rightarrow \rightarrow Y$:X,Y,Z是U的非空子集,Z=U-X-Y,对给定的(x,z),有一组Y与之对应,且Y只与x值有关而与z值无关,称Y多值依赖于X(X多值决定Y);
如:

数据依赖的公理系统
阿姆斯特朗公理系统
自反律:$Y\subseteq X\subseteq U$ --> $X \rightarrow Y$ (函数依赖的平凡性)
增广律: $X \rightarrow Y, Z\subseteq U$ --> $ XZ \rightarrow YZ$
传递律:$X \rightarrow Y, Y \rightarrow Z$ --> $X \rightarrow Z$
闭包
$ X^+_F $:属性集X在函数依赖F下的闭包,可以充分利用公理;
步骤:拆X,遍历地在逐个函数依赖中比较,加入可以推出的新的属性,直至某次遍历完成后没有加入任何属性为止;
例题:
最小覆盖(最小依赖集、正则覆盖)
定义判断:
- F中任一函数的右部仅含有一个属性;(右部多个属性的,由公理拆成一个属性的)
- F中不存在这样的函数依赖X→A,使得F与F-{X→A}等价。(对左部唯一的函数依赖,去掉任意一个都改变了原闭包)
- F中不存在这样的函数依赖X→A,X有真子集Z使得F-{X→A}∪{Z→A}与F等价。(所有函数依赖的左部都是最简的)
计算方法:
- 箭头右边,多个拆成一个
- 尝试性地去掉每个X->A,检查是否还能从$X^+_F$中推出A,等价就去掉X->A;(去掉多余的依赖)
- $X \rightarrow A$,对每个$ X = B_1B_2B_3\cdots B_m $,逐个考察每个$B_i$,如果去掉$B_i$,仍然能从$(X-B_i)^+_F$推出A,则用$X - B_i$替代X;(去掉各依赖左部多余的属性)
e.g. F={AB->C,C->A,BC->D,ACD->B,D->EG,BE->C,CG->BD,CE->AG}
- 右部属性单一化:{AB->C,C->A,BC->D,ACD->B,D->E, D->G, BE->C,CG->B, CG->D, CE->A, CE->G}
尝试性去掉每个X->A:
- 对AB->C
- 对C->A:去掉这个,C推不出A;
- ...
- {AB->C,C->A,BC->D,ACD->B,D->E, D->G, BE->C,CG->D, CE->G
模式分解
判断候选码的方法(trick)
- 如果有属性不在函数依赖集中出现,那么它必须包含在候选码中;
- 如果有属性只在函数依赖集右边出现,那么它必不包含在候选码中;
- 如果有属性只在函数依赖集的左边出现,则该属性一定包含在候选码中。
- 定义:如果有属性或属性组能唯一标识元组,则它就是候选码,也就是说,通过函数依赖所求出的候选码的闭包中(标记为$K_F^+ = U$),能够包含所有的属性。注意,当A是候选码时,所有包含A的属性组不再是候选码,因为这将与候选码的函数依赖定义冲突。
保持函数依赖的分解
步骤:
- 对R<U,F>的F求最小依赖集$F_C$,替代F;
- 找出所有不在F中出现的属性(记作$U_0$),把这样的属性记作$R_0<U_0,F_0>$,把这些属性从U中移除。
- 如果有:$X \rightarrow A \in F$,且$XA=U$,则ρ ={R},算法终止。
- 否则,对F按具有相同左部(函数依赖的左部)的原则分组(假定分为K组),每一组函数依赖所涉及的全部属性形成一个属性集Ui。若Ui⊆Uj(i≠j)就去掉Ui,于是ρ={R1<U1,F1>,…,Rk<Uk,Uk>}∪R0<U0,F0>构成R<U,F>的一个保持函数依赖的分解,并且每个Ri<Ui,Fi>均属于3NF。
- 至此,保留函数依赖的分解完成;
- 进一步考虑无损分解:判断分解后的关系模式中任何Ui是否含有码,若含有则为无损连接且保持依赖的3NF;否则,则是保持依赖但不是无损连接的3NF,此时需要新建一个关系模式,将码放入其中,具体操作为:新建$\tau = \{ R^*<X, F_\}$,其中X是候选码,$F_X$是F在X上的投影。将此关系放入$\rho$,得到保持依赖且无损连接的3NF;(!!投影的计算:如X:{A,B,C}, 那么A->B, A->C等只要在F中就属于Fx)
F: A->B A->C A->D B->C AB->C
事务和封锁
事务的ACID:原子性(Atomicity)、一致性(Consistency)、隔离性(Isolation)、持续性(Durability)
封锁
排他锁(写锁,X锁):只允许T读取与修改A;
共享锁(读锁,S锁):T可以读取A但是不能修改A,其他事务只可以对A加S锁而不能加X锁;保证了其他事务可以读取A,但在T释放S锁前不能对A做修改。
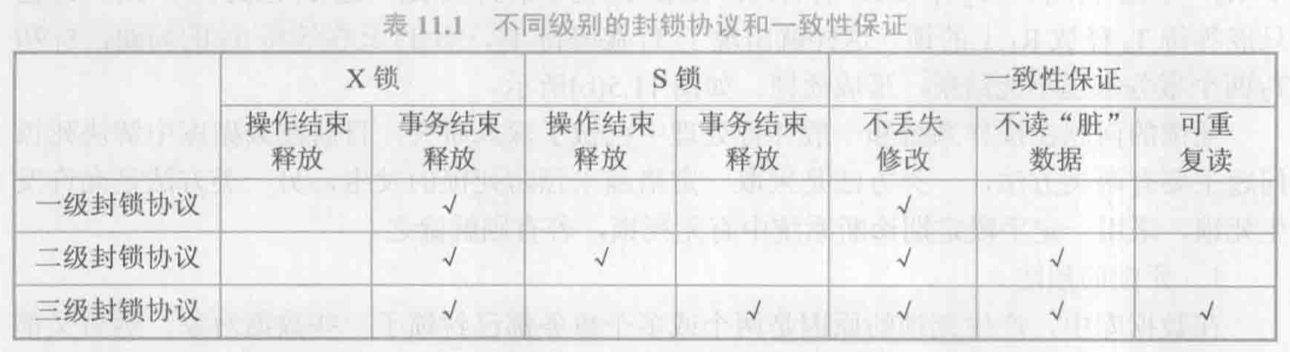
封锁协议
一级:T在修改数据前必须加X锁,事务结束后释放。
二级:在一级基础上,T在读取数据前必须加S锁,读完释放S锁;
三级:在一级基础上,T在读取数据前必须加S锁,事务结束后释放。
活锁:先来先服务预防饥饿
死锁预防:
- 一次封锁
- 顺序封锁
死锁诊断与排除:
- 超时
- 等待图
并发调度的可串行化:
- 可串行化调度:按照可串行化调度的执行顺序与串行调度的结果相同;
- 冲突操作:不同事物对同一个事务的读写、写写操作;
- 冲突可串行化:通过调换非冲突操作,将某个调度转换为串行调度,那么这个调度就是冲突可串行化的;冲突可串行化的调度都是可串行化调度($\rightarrow$,充分条件)
两段锁:对事务T,T必须分为两个阶段对数据项加锁:获得封锁的扩展阶段、释放封锁的收缩阶段。遵守两段锁协议的事务都是冲突可串行化的。与一次封锁法不同,两段锁可能遭遇死锁。
概念
- 数据独立性:数据域应用程序间的独立性,包括数据的物理独立性和逻辑独立性;数据独立性由DBMS三级模式之间的两层映象功能保证(外模式/模式映像使数据具有较高的逻辑独立性、模式/内模式映像使数据具有较高的物理独立性);
调度:事务的执行次序
- 串行调度:多个事务依次执行
- 可串行化调度:调度结果与串行执行这些事务时一致;
- 两段锁协议可以保证;
完整性:
- 实体完整性:主键不能取空值;
- 参照完整性:外键必须取被参照关系的主码值或空值;
- 用户自定义完整性:
- 数据字典
- 数据库设计的基本步骤:系统需求分析->概念设计(ER模型)->逻辑设计(关系模式)->物理设计->数据库实施->数据库运行和维护
- 日志文件:记录事务对数据库的更新操作;
- 事务的ACID:原子性(Atomicity)(要么全做,要么不做)、一致性(Consistency)、隔离性(Isolation)、持续性(Durability),并发控制子系统保证隔离性;
