KMP算法避免了朴素算法中指针的完全回溯，而是利用起了字符串失配后算法已知的信息，实现了待匹配串指针不回退，模式串指针回归由下文提及的next数组计算得出。

Reference

http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

https://blog.csdn.net/v_july_v/article/details/7041827

KMP的简略步骤：

• 求next数组（同一个pattern对应一组next数组）
• 利用next数组匹配

next数组的含义

部分匹配表（PMT, Partial Match Table）整体右移，首位补-1。

部分匹配表中存储了：对应元素前的子字符串的前后缀最大公共元素长度。

求解next数组的方法

    void GetNext(){
        next[0] = -1;
        int k = -1, j = 0;
        while(j < pat.length()){
            if(k == -1 || pat[j] == pat[k]){
                ++k;
                ++j;
                next[j] = k;
            }else{
                k = next[k];
            }
        }
    }

求解next数组的分析

我们利用递归思想，假设我们已知next[0]...next[j]，如何求取next[j+1]呢？

• 如果p[j] == p[k]，显然next[j+1] = next[j] + 1；
• 如果p[j] == p[k]，此时没有长度为k+1的前后缀公共子字符串，需要考虑能否找到更短的公共子字符串。我们这里运用k = next[k]递归求解k，这里的递归需要借助以下思路理解：
  

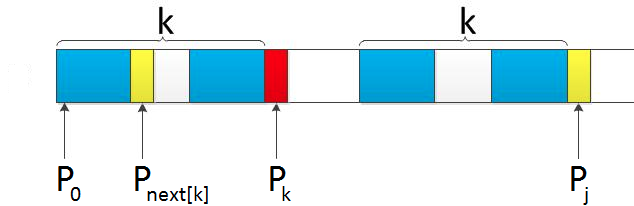
拿前缀$p_0, \cdots, p_{k-1}, p_k$和后缀$p_{j-k}, \cdots, p_{j-1}, p_j$匹配，如果$p_k,p_j$不匹配，下一步我们就要拿p[next[k]]与p[j]继续匹配，这个过程相当于字符串的自我匹配，可以通过k = next[k]的递归过程实现。

如何利用next数组匹配？

int KMPSearch(string src, string pat){
    int i = 0, j = 0;
    KMPPat p = KMPPat(pat);
    int sLen = src.size();
    int pLen = pat.size();
    while(i < sLen && j < pLen){
        if(j == -1 || src[i] == pat[j]){
            ++i;
            ++j;
        }else{
            j = p.next[j]; // 对应pat串右移j-next[j]
        }
    }
    if (j == pat.length()) return i-j;
    else return -1;
}

next数组决定了：当模式串中的某个字符跟文本串中的某个字符匹配失配时，模式串下一步应该跳到哪个位置。

如模式串中在j 处的字符跟文本串在i 处的字符匹配失配时，下一步用next [j] 处的字符继续跟文本串i 处的字符匹配，相当于模式串向右移动 j - next[j] 位。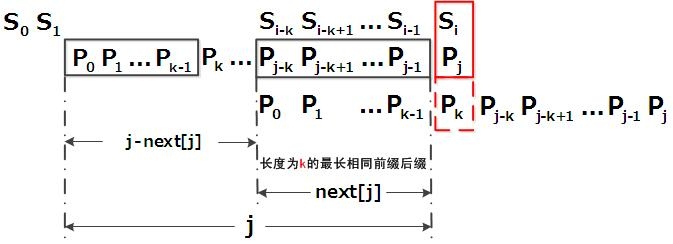

有关next数组的一些修正

上文中提到的求解next数组的办法尽管可用，但上一步过程中不应该出现p[j] = p[next[j]]，理由是：当p[j] != s[i] 时，下次匹配必然是p[ next [j]] 跟s[i]匹配，如果p[j] = p[ next[j] ]，必然导致后一步匹配失败（因为p[j]已经跟s[i]失配，然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配，很显然，必然失配）

当出现这种情况时，需要在再次递归，即next[j] = next[next[j]]

需要修改的代码段：

while(j < pat.length()){
            if(k == -1 || pat[j] == pat[k]){
                ++k;
                ++j;
                if(p[j] != p[k])  next[j] = k;
                else  next[j] = next[k];
             }else{
                k = next[k];
            }
        }

Tips: 如何利用KMP进行多次匹配

当pat指针j指向pLen时，模式串遍历完毕，证明匹配上了一串字符，此时存下索引$i-j$，然后继续利用j = next[j]递归即可。