去年12月第一次参加了CCF组织的CSP能力认证考试，不得不说没有受过专业程序设计训练的我参加这种考试时还是比较吃力的。下一次测试是在今年3月，而你拔CSP要求是260+，意味着这个寒假我得好好练习（各类骗分技巧）……
下面对本次CSP第三题做一次小复盘：

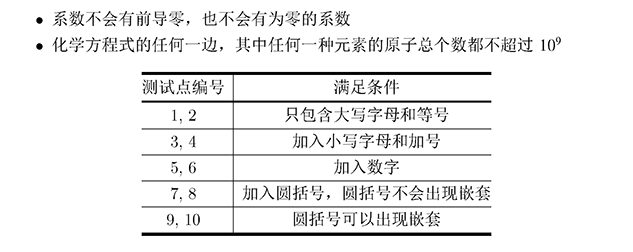
其实提供给出的BNF范式已经给了很大提示，只可惜尚未学习编译原理的我在场上很难静心琢磨了……下面给出大佬的逐步解析代码（实质上是LL语法分析中的递归下降）：

#include <bits/stdc++.h>
using namespace std;
const int N = 1001;
char equa[N];

int match(int k){ // 传入左括号  返回与其匹配的右括号的下标
    int c = 0;
    for(;;++k){
        if(equa[k] == '('){
            ++c;
        }else if(equa[k] == ')'){
            --c;
        }
        if(c == 0){
            return k;
        }
    }
}

void element(map<string, int> &mp, int coef, int l, int r){
    mp[string(equa + l, equa + r + 1)] += coef;
    // string的特殊构造方法：string(start, end), 与其他STL同样是左闭右开
}

void term(map<string, int> &mp, int coef, int l, int r){
    void formula(map<string, int> &mp, int coef, int l, int r);
    if(equa[l] == '(' && equa[r] == ')') {
        formula(mp, coef, l + 1, r - 1);
        return;
    }
    element(mp, coef, l, r);
}

void term_coef(map<string, int> &mp, int coef, int l, int r){
    if(equa[r] >= '0' && equa[r] <= '9'){
        int pos = r, num = 0;
        while(equa[pos] >= '0' && equa[pos] <= '9'){
            --pos;
        }
        for(int k = pos + 1; k <= r; k++){
            num = num * 10 + (equa[k] - '0');
        }
        if(num) coef *= num;
        term(mp, coef, l, pos);
        return;
    }
    term(mp, coef, l, r);
}

void formula(map<string, int> &mp, int coef, int l, int r){
    for(int i = l; i <= r; ){
        if(equa[i] == '('){
            int p = match(i) + 1;
            if(p > r){ // 括号是formula的最后一个字符  可以return
                // 如 Na(Au(CN)2)
                term_coef(mp, coef, i, p - 1);
                return;
            }
            while(equa[p] >= '0' && equa[p] <= '9'){
                ++p;
            }  // 括号后可能有下标，如(CN)2
            term_coef(mp, coef, i, p - 1);
            i = p;  // i的更新方式
        }else{
            int p = i + 1;
            while((equa[p] >= '0' && equa[p] <= '9') || (equa[p] >= 'a' && equa[p] <= 'z')){ // 跳过数字、小写字母
                ++p;
            }
            term_coef(mp, coef, i, p - 1);
            i = p;
        }
    }
}
void coef_formula(map<string, int> &mp, int l, int r){
    if(equa[l] >= '0' && equa[l] <= '9'){
        int coef = 0, pos = l;
        while(equa[pos] >= '0' && equa[pos] <= '9'){
            coef = coef * 10 + (equa[pos++] - '0');
        }
        formula(mp, coef, pos, r);
        return;
    }
    formula(mp, 1, l, r);
}

map<string, int> expr(int l, int r){
    map<string, int> mp;
    int pre = l;
    for(int i = l; i <= r; i++){
        if(equa[i] == '+'){
            coef_formula(mp, pre, i - 1);
            pre = i + 1;
        }
    }
    coef_formula(mp, pre, r);
    return mp;
}

int main(int argc, char** argv) {
    int n;
    scanf("%d", &n);

    for(int i = 0; i < n; i++){
        scanf("%s", equa);
        int e = find(equa, equa + N, '=') - equa;
        printf(expr(0, e - 1) == expr(e + 1, strlen(equa) - 1) ? "Y\n" : "N\n");
    }
    return 0;
}