之前我们学习了如何用MLP实现手写数字识别并达到了95%左右的准确率。在介绍卷积神经网络之前，我简单地了解了一下k-NN也就是大部分人耳熟能详的K最近邻算法。像往常一样，本文注重对算法思想的理解而不会纠结于数理公式的推导。
本文及其系列图表信息大都来自Stanford CS231n系列课程，也算作我的听课笔记吧。

算法原理

我们知道，逻辑回归是一个分类器，K最近邻算法也是。所谓最近邻，就是采用多数投票的方式，“测量”单个测试集样本到训练集样本的“距离”，取其中最近的k个，这k个中哪个类别的训练样本最多，我们就认为此测试样本属于这一类。
简单来说就是：计算距离→取K个→多数投票判断类别

距离

总的来说，K近邻算法中的距离，也是闵可夫斯基距离，(Minkowski Distance)可由下式表示：
$$ D(x,y)=(\sum_{i=1}^m|x_i-y_i|^p)^{\frac{1}{p}} $$
当p=1时，我们称其为曼哈顿距离（Manhattan Distance），又称L1距离，表达式为$ d_{1}(I1,I2)=\sum_{p}|I_{1}^p-I_{2}^p| $。
当p=2时，我们称其为欧几里得距离（Euclidean Metric），又称L2距离，表达式为$ d_{2}(I1,I2)=\sqrt{\sum_{p}I_{1}^2-I_{2}^2} $

举例

以图像分类为例，假如说我们要判断一张32x32大小的灰度图片中是否有猫，训练集是10000张有猫的图片与10000张没有猫的图片。可以说，对k-NN算法没有训练这个过程，或者“此训练非彼训练”，最近邻算法中的训练只是简单地记忆，测试环节才是大头。

对给定的任意一张测试图片，以L1距离为例，我们要做的只是将测试图片灰度值矩阵与训练样本灰度值矩阵作差，并将得到的新矩阵元素全部作和，得到L1距离。对20000个训练样本如法炮制，找到距离最近的k个，其中如果投票“猫”的训练集样本多，我们就说k-NN算法认为测试图片中有猫。大概像这样：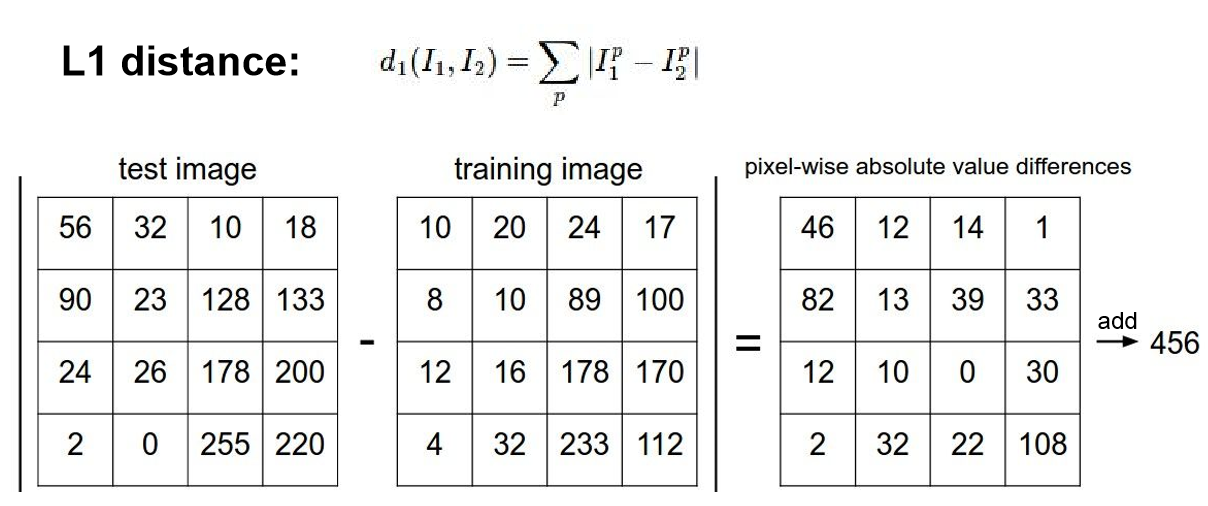

拓展

k-NN算法看起来太简单了，无论是计算机科学家还是数学家们都希望在其之上作出一些改进，如ANN（Approximate Nearest Neighbor），有兴趣的可以自行搜索。

超参数选择

在这个算法中，可供选择的超参数并不多。

L1 or L2？

现在来看，具有直观几何意义的L2即欧氏距离效果较好，当然也推荐在具体的项目上实操一下。

k的选择

遗憾的是，即便是对于数学原理如此简单的k-NN算法（相比MLP与CNN），超参数的选择仍然取决于实际问题，因此人们有时会作出这样的图像帮助选择参数k。

这里有一个小细节，上图制作的方法并不是死板地在数据集中分割出测试集与训练集，而采用交叉验证（Cross Validation）方法得出最佳k的选择。
什么意思呢？例如说10000张训练集，1000张测试集，我并不死板地在每次测试中载入所有训练样本，而是少量多次得到多个结果，平均后作为某一个k值的最终结果，划分的小样本集称作验证集（Validation Set）。
事实上，交叉验证是在机器学习建立模型和验证模型参数时常用的办法。有关交叉验证还有许多结合概率论与统计学原理的升级版，可以移步《交叉验证(Cross Validation)原理小结》原理小结》")。

遗憾

k-NN作为平常的分类器，在数据处理方面能以较小的计算量脱颖而出（手算k-NN和手算CNN你选一个吧，手动滑稽），但其在图像方面表现惨不忍睹，所以我上文举的例子完全是便于理解用的，没有人会将k-NN算法应用于图像。
为什么呢？这取决于“距离”一词在图像上十分不可靠、与直觉不相符（unintuitive）。
例如说这样四幅图片，难以想象右边三幅到最左边一幅的L2距离完全相同！

这样来看，k-NN在图像上表现不佳也变得没那么难理解了……（眼睛嘴巴都没了还看不出来玩锤子）