在没有CNN以及更加先进的神经网络的时代，多层感知机（下文简称MLP）是图像识别、图像分类比较传统的方法之一。尽管这类方法出现于上世纪八九十年代，但不妨碍我们对其进行进一步学习。（小声说：微积分还是几百年前的呢……）
参考：Using neural nets to recognize handwritten digits
本文结合通过MNIST手写数字识别项目的实现 了解多层感知机（MLP）的小细节食用更佳！

（笑话：这是你的机器学习系统吗？对呀！你把数据倒进这堆线性代数，然后再另一头等着答案就成！要是答案是错的呢？搅一搅这堆线性代数，搅到看上去对了为止。）

什么是神经网络？

神经网络因采用了与人脑类似的网络结构而得名，但其与真正人脑的运作原理不尽相同。我们今天介绍一种最简单的神经网络——多层感知机。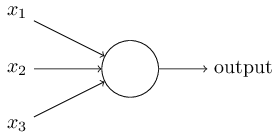

图中的单个感知机有三个输入，左端的三条线对应三个权重（weights），我们要做的是用输入乘以对应的权重并求和，即计算$\sum_{i}w_{i}x_{i}$。如果结果大于某个阈值，output=1，否则output=0。单个简单感知机与人的神经元十分类似：高中生物提到过，神经元只有类似二进制的激发态与非激发态。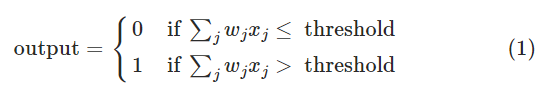

用一个简单的例子来思考一下：假如你喜欢的明星开了一场演唱会，你正在思考是否要去，你去之前可能会权衡一下以下问题：

1. 天气咋样？
2. 女朋友愿不愿意陪？（滑稽）
3. 交通便利吗？

假如这三个问题代表了三个输入，问题得到肯定答复输入为1，否则为0；而且三个问题的“重要性”不一定一致：显然女朋友重要性要更高，不妨把其权重设为6，其他两个看上去没有那么重要依次设为2和3。这样，在做决定之前这样计算一次，你就能得到一个答案。
显然，这并不是人脑做决定的真正模型，但如果并不止一个感知机呢？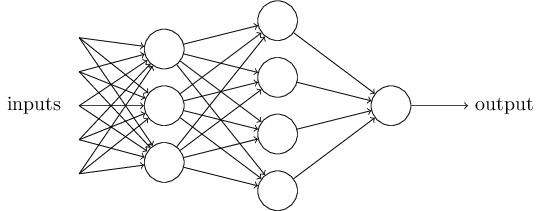

正如你所见，多个感知机可以构成一层（layer）网络，网络与网络之间可以叠加。我们不妨简化一下感知机的表达形式：令b为上述的阈值，称之为偏置（bias）；w为权重值组成的行向量，x为输入组成的列向量，那么上述公式可以简化为：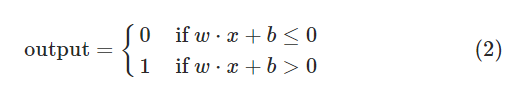

可以证明，感知机网络可以用来构成逻辑电路，进而进行任意类型的逻辑计算，但这与本文内容脱节，在此不予介绍，你只需要知道感知机网络理论上可以实现任何逻辑任务。

利用多层感知机 理解识别手写数字项目

想象一下现在有一个28维方阵，每个元素装着对应像素点的灰度值，像这样：

这784个元素排成一排，构成了神经网络的第一层，作为神经网络的输入，每个元素中装着的数字叫神经元的激活值。

数字一共有10个，所以神经网络最后应该对应10个输出的激活值，每一个输入都会对应10个激活值，激活值最大的那一项应该就是MLP的判断结果。
PS：若是要对应十个数字，4个输出已经足够($2^4=16>10$),但为何要用10个输出呢？请读者思考。
问题来了：

1. 中间的隐含层有何意义？
2. 怎么由上一层的激活值计算下一层的激活值？

隐含层的意义

我们期待，如果每一层网络都能实现一些功能，比如说对这幅图片：
人脑一看就知道是数字0，但从理论算法的角度来看，传统算法并不好对付这样的手写数字识别问题，即使可以处理，算法的健壮性也不足以投入生产。
假如网络的层数足够多，我们能不能让每一层都实现将单幅图片拆分成如下几部分？

如果可以，我们能想象只要第二层中代表这四个部分的神经元激活值很高，输出结果大概率是0即可。
这样的思路显然也可用于拆分其他数字：

这样一想，MLP算法应该可以广泛用于所有图像识别领域，甚至在音频识别、NLP领域都能打出一番天地，因为上述领域都能拆分为一小块一小块逐份处理。当然其不佳的准确率与性能表现导致被CNN等后来者居上，但理解MLP仍然是深度学习领域“HelloWorld”形式的存在。

例如：我们用第二层网路的一个神经元判断图像上的这个部位是否有一横，只需要将这一横所对应的神经元权重设为正的（图中的绿色色块），周围的神经元设为负的（图中的红色色块），这样当图像中出现类似一横的图像时，第二层网络的激活值将会很大，从而使这个神经元被点亮（fired）。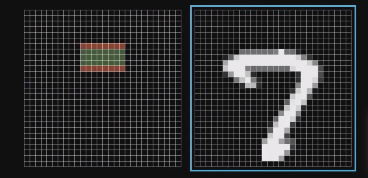

这下问题又来了：
1、这样计算出来的激活值可以是任意实数，而我们需要的只是0~1范围的激活值，这里牵涉到激活函数。
2、难道我们要手动调整这些权重与偏置吗？

激活函数

下面是常见的激活函数表达式及图像：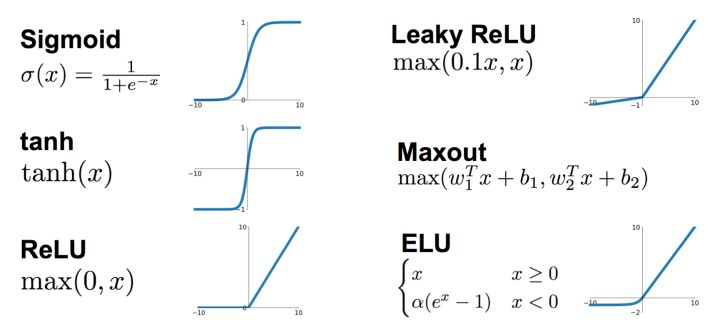

本例中选用sigmoid函数作为激活函数，尽管在实践中sigmoid函数被证明存在诸多缺点，但不影响本例的实现。实际应用中应根据需要选择，当然目前常用的是ReLu函数。
Sigmoid函数能将十分大和十分小的输入分别逼近至0,1，而在输入0附近的数时平滑变化。
这样我们可以用这种简化形式表达各层之间激活值的转换，这对简化我们的程序有重要的作用：

为什么要使用激活函数？

使用激活函数的目的仅仅是将任意实数缩小至0~1范围吗？显然不是。

权重与偏置的调整

经过计算，上图中简单的四层网络共有13002个参数（包括权重与偏置）可供调整，要是真的手动调整……一言难尽……
其实一开始我们会给这些参数随机分配值，可以想象随机分配的参数实现的神经网络的效果一定不堪设想，这时候就要祭出机器学习大杀器——机器如何学习？

学习首先得有数据，还得是已经知道结果的、标注好的数据。

将标注好的数据逐个送入随机参数的神经网络，网络大概率会给出一个错误结果，问题来了：如何通过多个错误结果逐步逼近至正确结果呢？

损失函数（对单个样本而言）、代价函数（对训练集而言）

大学英语第一册中有一篇文章提到：书中每多一个公式，书的销量就会打上五折。可惜的是对机器学习这种与数学不分家的领域不牵涉数学知识很难理解透彻一个概念。
损失函数就是给矫正参数提供数据的，损失函数因不同的算法而异，本项目运用的是简单的平方和损失公式。

而之前我在项目《YOLOv3-基于Python的高空监控识别与目标检测系统|我在参加五粮春杯作品类竞赛的历程》用过的YOLOv3的损失函数：

无论是哪种损失函数，它都要符合一个原则：当网络能对图像进行正确分类时，损失函数值要比较小，偏差的越大，损失值越大。
对所有样本的损失函数值的平均函数称为代价函数，当然如今包括很多学术论文已经不再区分两个概念。

代价函数相当于以13002个参数为输入，输出一个cost值来表示神经网络的表现，而参数则是你提供的各个训练图片。

如果只知道网络的表现如何糟糕，对网络识别率的进步没有任何帮助，就像家长总骂孩子“你咋这么笨”而不告诉其如何改正一样。

那么该如何修正神经网络的参数呢？

梯度下降法

先抛开自变量众多的代价函数，我们先看看如何求解一元函数的最小值，其方法在任意一本微积分教材上应该都有：计算导数为0的点，确定极小值，计算极小值中的最小值。
但有时你会发现，函数十分复杂时的求导与最小值求解不是那么方便，更不用提13002元函数了。

更巧妙的方法是：随便挑一个输入值，然后判断，向左走还是向右走函数值才会变小呢？如果随机的这一点处斜率为正，向左走一点能让函数值变小；如果斜率为负那么就向右走一点。走的时候还需要注意：斜率越平缓时走的每一步应该越来越小，这样可以保证不会“走过头”而越过极小值点。

这有点像在一元函数图像上放上许多个小球，每个小球最终都会停在一个“坑里”，这就是函数的极小值“坑”。

问题来了：极小值点不一定是最小值点，神经网络也会遇到高等数学解题中同样的问题，需要注意。

让我们再拓展到二元函数：类比一元函数，在二元函数的图像中我们要思考的应该是“哪个方向下山最快？”，尽管尚未接触二元函数知识，但我们知道，按梯度的方向走，函数值增长的最快，那么按梯度的反方向，函数就减少的最快咯，而且梯度向量的长度代表了这个最陡的斜坡到底有多陡。
这样我们就得到了一种让函数值最小的算法：计算梯度→按梯度反方向调整自变量→循环，这对以13002个自变量为输入的代价函数也是一样，将所有输入作为13002维的列向量并计算负梯度并加在列向量上就能计算出调整后的神经网络参数。

需要注意的是，代价函数是对训练集而言，也就是很可能出现这样一种情况：随机的参数在特定输入上得到了正确答案，但训练后的参数反而给出了错误的答案，这是因为上述梯度下降的过程是针对所有样本而言的，训练后的参数对所有样本得到的总体结果会更好一些。

计算多元函数的梯度

问题又来了……如何计算多元函数的梯度？方法叫做反向传播，这个留在下一篇博文再讲，暂时不理解也不影响理解本文。

隐含层起到了预想的效果吗？

我们起初是想隐含层能分开识别数字的不同组件，但上述方法我们压根没有接触到怎么样识别数字的不同组件，例如什么“9”就是上面一个圈下面一竖线的逻辑。而事实上的确隐含层并没有使用我们想让它那样的逻辑，而是在万千数字海洋中利用梯度下降找到了个不错的“极小值点”住了下来并且达到了不错的效果，这就是为什么说神经网络模型是个小黑盒：效果不错，原理明白，为啥这样我也将不太清楚。

事实上，这个网络尚没有我们想象的那么智能，例如输入一张乱码图片，我们期待它给出10个差不多的激活值；但恰恰相反它会“神经质般”地认定输入的图片就是“4”。在它到他的路上，众多计算机科学家与数学家还有漫长的道路要走。

后续

本文粗略地以大一新生的视角介绍了MLP算法中的关键点（除了反向传播，将另开文记录），可能部分地方有失偏颇，欢迎评论指出，在寒假阶段我还会继续了解更多机器学习概念并记录分享。