本文将在结合手写数字识别项目 深入理解多层感知机(Multi-Layer Perceptron)的基础上深化细节的解释,查漏补缺,而并不像之前那样拘泥于理解。
思考题答案
前文提到10个数字应该只需要4个输出神经元足矣,为何设计10个,是否会涉及到效率与性能问题呢?答案有些经验主义:你都试试嘛!在这个特别的问题上,数据表明10个神经元的输出层准确度较高。至于深层的原因,前文已经提到过我们想让每个隐藏层识别出不同的数字部分,而显然四个神经元的二进制组合输出很难达到我们的要求。
当然你如果对4个神经元的输出有一股执念,你也可以这么玩: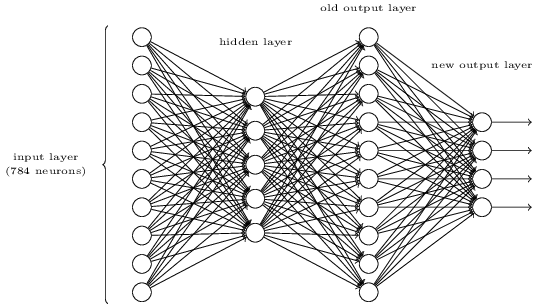
给你留个作业:找到第三层与至四层之间的一组权重与偏置,使得输出有对应关系。(假如第三层输出的正确答案激活值大于0.99,错误的激活值小于0.01)计算的过程中你会有一种计算机多么伟大的感慨。
概念关系
单层感知机、多层感知机、Sigmoid神经元
在前文的介绍中,这样的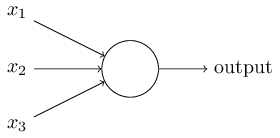 被称作单层感知器,而MLP则由任意层数的单层感知器叠加而成。本例中涉及的MLP使用的激活函数,而是sigmoid函数,所以有的文章将这样的MLP的基本单位称作sigmoid neurons(sigmoid神经元)。
被称作单层感知器,而MLP则由任意层数的单层感知器叠加而成。本例中涉及的MLP使用的激活函数,而是sigmoid函数,所以有的文章将这样的MLP的基本单位称作sigmoid neurons(sigmoid神经元)。
单层感知器与sigmoid神经元的最大区别是sigmoid输出连续,而单层感知机只输出0和1。这样我们也很容易想到:
- 将单层感知机构成的网络中的权重与偏置全部乘以一个正的常数c,显然神经网络的行为不会改变。
- 假如对上面所提的网络的输入已经确定,且所有神经元的激活值均不为0。现在将所有感知机换为sigmoid神经元,同样将网络中的权重与偏置乘以一个无穷大的常数c,显然调整前与调整后的网络行为不会改变。
神经网络的结构、隐藏层、前馈神经网络
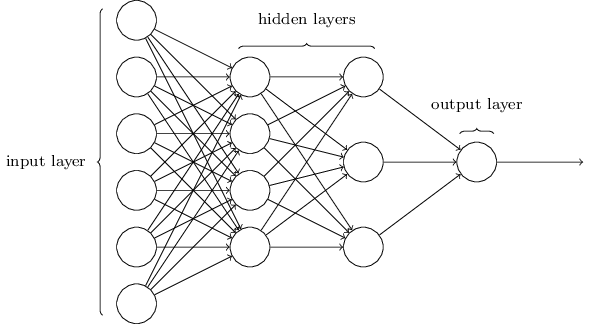
上图的MLP网络结构之前已经介绍过,其中“隐藏层”得名于其既不是输入层也不是输出层,并无其他含义。隐藏层的设计并没有特定要求,通常通过试验不同的隐藏层来取得最佳效果,输入层与输出层的设计也十分直接。
这种将上一层的输入当做下一层的输出的神经网络称为前馈神经网络(feedforward neural networks),其中前馈之意就是网络中没有循环——信息永远向前传递而不回头走。乍一看如果数据还能回着走岂不是乱了套?谁知有一种叫循环神经网络(recurrent neural networks)的模型,以后有机会可以介绍。
梯度下降法的公式描述、随机梯度下降(SGD)与学习率
之前用通俗的小球语言解释了梯度下降法,下面我尝试用数学方法解释一下。

对多元函数采用梯度下降法计算量大,上面介绍了随机梯度下降。
有时人们在代价函数中省略训练集大小n,因为有时训练集大小并不固定(各行各业每时每刻都在产生数据),自然地有时上面的公式中省略批大小m。这就要求在训练过程中相应的缩放学习率的大小。
随机梯度下降得到的梯度向量不一定精确,但我们不需要它绝对的精确——只要它的负向量指向C减少的方向即可。
随机梯度下降的极端情况是batch大小为1,这样每次只取出一个样本用来计算,请思考:这样会带来怎样的好处和后果?
迭代(iteration)与迭代次数(epoch)
举个简单的例子理解随机梯度下降中的这两个概念:假如训练数据有10000条,batch_size定为10,那么10000条全部过一遍称为完成了1000次iteration,1 次epoch。
代码实现
初始化网络
这里我们定义一个类Network:
class Network(object):
def __init__(self, sizes):
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]] # 随机生成偏置 注意从第二层开始才需要偏置(批注1)
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])] # 随机生成权重(批注1)用法:net = Network([2, 3, 1])代表创建一个第一层有两个神经元,第二层有三个神经元,第三层有一个神经元的Network对象。
np.random.randn函数将会随机生成以0为均值,1为标准差的标准正态分布数据。以后我们会接触到更合理的权重初始化方式,但如今我们先凑活用一下。
np.random.randn函数的标准形式为numpy.random.randn(d0,d1,…,dn),没有参数时返回单个随机数,有一个参数时返回秩为1的数组,有两个及以上参数时返回对应维度的数组,可以表示向量和矩阵。参数的个数代表数组的维度,参数的数值代表对应维数的数据个数,如numpy.random.randn(3,1)表示生成一个二维数组,第一维有三个数据,第二维有一个数据。生成的数组自然也能用下标方式访问,举例如下:
>>> a=np.random.randn(3,1)
>>> print (a)
[[ 1.90478059]
[-0.96366796]
[ 1.76571214]]
>>> a[0]
array([1.90478059])
>>> a[0][0]
1.9047805907019604批注1:还是看看这张图:
显然input layer这一层不需要偏置,因为数据直接输入;而矩阵net.weights[k]则代表k+1层到k+2层的权重,这看上去有些别扭,不如就把net.weights[k]看做矩阵W,矩阵元素Wab代表k+1层的第b个神经元到k+2层的第a个神经元的权重。
Wab这样的表达有点怪怪的,这样做的好处是前馈过程很容易用以下公示表达出来:$ {a}'=\sigma \left ( wa+b \right ) $for x, y in zip(sizes[:-1], sizes[1:])可能有点难以理解,首先zip是将两个列表合并并构成元组对,如此例:
>>> sizes = [2,3,4,5,6,7]
>>> for x, y in zip(sizes[:-1], sizes[1:]):
print (x,y)
2 3
3 4
4 5
5 6
6 7
>>> list(zip(sizes[:-1],sizes[1:])) # zip不能直接显示
[(2, 3), (3, 4), (4, 5), (5, 6), (6, 7)]或许用一张手绘图更好理解:
定义sigmoid函数
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))在Network类中加入前馈函数
def feedforward(self, a):
"""Return the output of the network if "a" is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b) # 注意做点积的做法
return a随机梯度下降
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""用小批次随机梯度下降训练神经网络 "training_data" 是元组
"(x, y)"的列表, 代表训练输入和期望输出 其他的必要参数不言自明
如果提供了test_data那么网络将会在每一次epoch后根据test_data进行评估并打印部分过程
这对跟踪进程很有用,但会拖慢训练速度 """
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs): # 批注1
random.shuffle(training_data) #随机排序列表
mini_batches = [training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] # 随机排序完成后取出需要的小批次作为一个列表
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)批注1:xrange与range用法基本一致,不同在于xrange作为一个生成器,不能用来生成列表,但xrange性能优化很多,比如这样的做法是错误的:x = list(xrange(5))
update_mini_batch函数
def update_mini_batch(self, mini_batch, eta):
"""通过对一个小批次应用梯度下降(使用反向传播算法)更新网络的权重与偏置
"mini_batch" 是(x,y)元组 eta是学习率 """
nabla_b = [np.zeros(b.shape) for b in self.biases] # 用0填充与偏置维数相同的列表
nabla_w = [np.zeros(w.shape) for w in self.weights] # 用0填充与权重维数相同的列表
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]注意这一行:delta_nabla_b, delta_nabla_w = self.backprop(x, y),其中的backprop就是著名的计算多元函数梯度的反向传播算法了,我会另开文介绍。
上面这部分与公式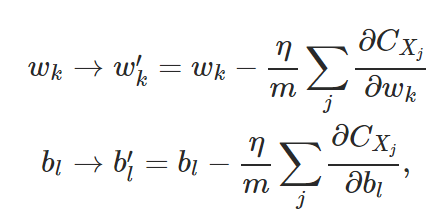 相对应。
相对应。
加载MNIST数据集
计算方法在这里就介绍完了,下面介绍一下如何处理MNIST数据集。
import cPickle
import gzip
import numpy as np
def load_data():
"""返回一个包含``(training_data, validation_data,
test_data)``的元组.
``training_data`` 是一个包含50000个2维元组的列表 ``(x, y)`` ``x`` 是784维的numpy.ndarray包含图像信息
``y`` 是10维numpy.ndarray代表x中装着的正确数字
``validation_data`` 和 ``test_data`` 是包含10000个2维元组的列表 ``(x, y)``.
``x`` 是784维numpy.ndarry包含输入图像 ``y``是对应的分类(整数形式)
从此可以看出training_data与验证集和测试集数据结构有些许差异"""
f = gzip.open('../data/mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return (training_data, validation_data, test_data)
def load_data_wrapper():
"""Return a tuple containing ``(training_data, validation_data,
test_data)``. Based on ``load_data``, but the format is more
convenient for use in our implementation of neural networks.
In particular, ``training_data`` is a list containing 50,000
2-tuples ``(x, y)``. ``x`` is a 784-dimensional numpy.ndarray
containing the input image. ``y`` is a 10-dimensional
numpy.ndarray representing the unit vector corresponding to the
correct digit for ``x``.
``validation_data`` and ``test_data`` are lists containing 10,000
2-tuples ``(x, y)``. In each case, ``x`` is a 784-dimensional
numpy.ndarry containing the input image, and ``y`` is the
corresponding classification, i.e., the digit values (integers)
corresponding to ``x``.
Obviously, this means we're using slightly different formats for
the training data and the validation / test data. These formats
turn out to be the most convenient for use in our neural network
code."""
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)
def vectorized_result(j):
"""Return a 10-dimensional unit vector with a 1.0 in the jth
position and zeroes elsewhere. This is used to convert a digit
(0...9) into a corresponding desired output from the neural
network."""
e = np.zeros((10, 1))
e[j] = 1.0
return e使用
如果你懒,不想理解代码的细节,就可以直接跳到此处从GitHub上把代码拉下来玩。git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git
玩法如下:
Python 2.7.15 (v2.7.15:ca079a3ea3, Apr 30 2018, 16:30:26) [MSC v.1500 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network
>>> net = network.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
Epoch 0: 8193 / 10000
Epoch 1: 9193 / 10000
Epoch 2: 9215 / 10000
Epoch 3: 9327 / 10000
Epoch 4: 9298 / 10000
……
Epoch 17: 9489 / 10000
Epoch 18: 9498 / 10000
Epoch 19: 9504 / 10000
Epoch 20: 9495 / 10000
Epoch 21: 9498 / 10000
Epoch 22: 9487 / 10000可以看到尽管只是几十行代码的小玩意,在测试集上的准确率也有94%左右,随后我们接触到的卷积神经网络(CNN)可以把这个数据提升至99%!想想就令人激动!
关于参数、超参数
神经网络中涉及到参数(parameters)与超参数(hyper-parameters),这两个概念很好区分:
- 参数是神经网络通过学习自己调整的,比如文中的权重与偏置,是不需要人工干预的。
- 超参数往往是训练过程的一些参数,比如文中的学习率、迭代次数等。超参数的调整有些经验主义,神经网络的调参过程几乎与神经网络的结构设计同样重要,比如迭代次数过大会引起过拟合(在训练集上准确率高,但在测试机上准确率堪忧)。说我们在本例的基础上玩一些花样:
# 花样1:修改MLP结构
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
# 花样2:修改学习率
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data)
2 comments
“假如对上面所提的网络的输入已经确定,且所有神经元的激活值均不为0。现在将所有感知机换为sigmoid神经元,同样将网络中的权重与偏置乘以一个非无穷大的常数c,显然调整前与调整后的网络行为不会改变。”为什么要限定所有神经元的激活值均不为0 呢?
个人理解是,激活值为0的神经元在后续的线性计算中不能起到效果,类似被dropout了。