特征值和特征向量的定义如下:
$$Ax=\lambda x$$
其中A是一个$n×n$的实对称矩阵,$x$是一个n维向量,则我们说$λ$是矩阵A的一个特征值,而$x$是矩阵A的特征值λ所对应的特征向量。
实特征值的几何意义:我们知道,向量右乘方阵对应了一种线性变换,在这个变换过程中,向量会发生旋转、伸缩或镜像的变化。特征向量的定义即为:如果矩阵A对向量x只起到了伸缩的效果(仍在x张成的子空间上),那么这些向量就是矩阵A的特征向量,伸缩的比例就是特征值。
求解特征值与特征向量的步骤:
- 解特征方程: $|A−λI_{n} |=0$
- 把每个特征值代入线性方程组$(A−λE)x=0$,求出基础解系。
- 求得的基础解系张成的特征子空间中所有向量均为对应特征值的全部特征向量。
求出特征值与特征向量后,我们可以将A进行特征分解,即对矩阵A的n个特征值$λ_1≤λ_2≤…≤λ_n$ ,以及其对应的特征向量$\{w_1,w_2,...w_n\}$,如果这n个特征向量线性无关,矩阵A可以分解为以下形式:
$A=W∑W^{-1}$
其中W是这n个特征向量所张成的n×n维矩阵,而Σ为这n个特征值为主对角线的n×n维矩阵。
注意到要进行特征分解,矩阵A必须为方阵。那么如果A不是方阵,即行和列不相同时,我们还可以对矩阵进行分解吗?
答案是肯定的,需要用到SVD奇异值分解。
奇异值分解没有出现在我校线性代数课本中,此处引用《奇异值分解(SVD)原理与在降维中的应用》原理与在降维中的应用》")
奇异值分解
奇异值分解不要求A为方阵,不失一般性,设其为$m \times n$的矩阵,定义矩阵A的SVD为:
$$ A = U\Sigma V^T $$
其中U是一个$m \times m$的矩阵;$\Sigma$ 是一个$m \times n$的矩阵,除了主对角线上的元素以外均为0,主对角线上的每个元素称为奇异值(非方阵的主对角线以min(m,n)为基准);V是一个$n \times n$的矩阵。
U和V都是酉矩阵,即满足$U^{T}U = I, V^{T}V = I$。
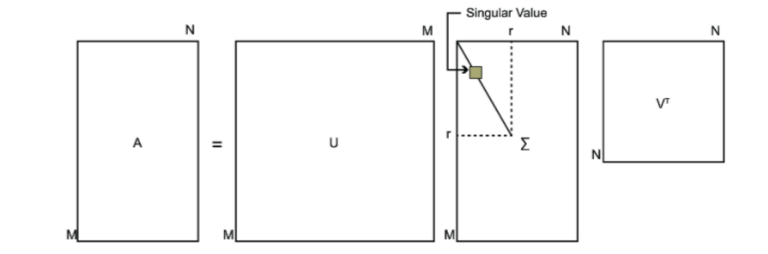
如何求出SVD分解后的U,Σ,V这三个矩阵呢?
如果我们将A的转置和A做矩阵乘法,那么会得到$n×n$的一个方阵$A^{T}A$。既然$A^{T}A$是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
$$(A^{T}A)v_{i} = \lambda_{i}v_{i}$$
这样我们就可以得到矩阵$A^{T}A$的n个特征值和对应的n个特征向量v了。将$A^{T}A$的所有特征向量张成一个n×n的矩阵V,就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
如果我们将A和A的转置做矩阵乘法,那么会得到$m×m$的一个方阵$AA^{T}$。既然$AA^{T}$是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
$$(AA^T)u_i = \lambda_i u_i$$
这样我们就可以得到矩阵$AA^{T}$的m个特征值和对应的m个特征向量u了。将$AA^{T}$的所有特征向量张成一个m×m的矩阵U,就是我们SVD公式里面的U矩阵了。
一般我们将U中的每个特征向量叫做A的左奇异向量。
U和V我们都求出来了,现在就剩下奇异值矩阵Σ没有求出了。由于Σ除了对角线上是奇异值其他位置都是0,那我们只需要求出每个奇异值σ就可以了。
我们注意到:
$$A=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i = \sigma_i u_i \Rightarrow \sigma_i = Av_i / u_i$$
这样我们可以求出我们的每个奇异值,进而求出奇异值矩阵ΣΣ。
上面还有一个问题没有讲,就是我们说$A^{T}A$的特征向量组成的就是我们SVD中的V矩阵,而$AA^{T}$的特征向量组成的就是我们SVD中的U矩阵,这有什么根据吗?这个其实很容易证明,我们以V矩阵的证明为例。
$$A=U\Sigma V^T \Rightarrow A^T=V\Sigma^T U^T \Rightarrow A^TA = V\Sigma^T U^TU\Sigma V^T = V\Sigma^2V^T$$
上式证明使用了:
$U^TU=I, \Sigma^T\Sigma=\Sigma^2$。
可以看出$A^{T}A$的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到$AA^{T}$的特征向量组成的就是我们SVD中的U矩阵。
进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:$\sigma_i = \sqrt{\lambda_i}$
这样也就是说,我们可以不用
$\sigma_i = Av_i / u_i$来计算奇异值,也可以通过求出$A^{T}A$的特征值取平方根来求奇异值。
