今天学习的是用一组各类花费与盈利呈线性关系的数据集训练多元线性回归模型,感觉这一系列教程涉及的全是代码和实现,原理方面牵涉的很少,看来要私下补一下。
第1步:数据预处理
导入库
import pandas as pd
import numpy as np导入数据集
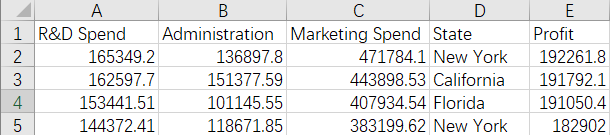
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[ : , :-1].values
Y = dataset.iloc[ : , 4 ].values
print(X[:10])
print(Y)[[165349.2 136897.8 471784.1 'New York']
[162597.7 151377.59 443898.53 'California']
[153441.51 101145.55 407934.54 'Florida']
[144372.41 118671.85 383199.62 'New York']
[142107.34 91391.77 366168.42 'Florida']
[131876.9 99814.71 362861.36 'New York']
[134615.46 147198.87 127716.82 'California']
[130298.13 145530.06 323876.68 'Florida']
[120542.52 148718.95 311613.29 'New York']
[123334.88 108679.17 304981.62 'California']]
[192261.83 191792.06 191050.39 182901.99 166187.94 156991.12 156122.51
155752.6 152211.77 149759.96 146121.95 144259.4 141585.52 134307.35
132602.65 129917.04 126992.93 125370.37 124266.9 122776.86 118474.03
111313.02 110352.25 108733.99 108552.04 107404.34 105733.54 105008.31
103282.38 101004.64 99937.59 97483.56 97427.84 96778.92 96712.8
96479.51 90708.19 89949.14 81229.06 81005.76 78239.91 77798.83
71498.49 69758.98 65200.33 64926.08 49490.75 42559.73 35673.41
14681.4 ]将类别数据数字化
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[: , 3] = labelencoder.fit_transform(X[ : , 3])
print("labelencoder:")
print(X[:10])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()
print("onehot:")
print(X[:10])labelencoder:
[[165349.2 136897.8 471784.1 2]
[162597.7 151377.59 443898.53 0]
[153441.51 101145.55 407934.54 1]
[144372.41 118671.85 383199.62 2]
[142107.34 91391.77 366168.42 1]
[131876.9 99814.71 362861.36 2]
[134615.46 147198.87 127716.82 0]
[130298.13 145530.06 323876.68 1]
[120542.52 148718.95 311613.29 2]
[123334.88 108679.17 304981.62 0]]
onehot:
[[0.0000000e+00 0.0000000e+00 1.0000000e+00 1.6534920e+05 1.3689780e+05
4.7178410e+05]
[1.0000000e+00 0.0000000e+00 0.0000000e+00 1.6259770e+05 1.5137759e+05
4.4389853e+05]
[0.0000000e+00 1.0000000e+00 0.0000000e+00 1.5344151e+05 1.0114555e+05
4.0793454e+05]
[0.0000000e+00 0.0000000e+00 1.0000000e+00 1.4437241e+05 1.1867185e+05
3.8319962e+05]
[0.0000000e+00 1.0000000e+00 0.0000000e+00 1.4210734e+05 9.1391770e+04
3.6616842e+05]
[0.0000000e+00 0.0000000e+00 1.0000000e+00 1.3187690e+05 9.9814710e+04
3.6286136e+05]
[1.0000000e+00 0.0000000e+00 0.0000000e+00 1.3461546e+05 1.4719887e+05
1.2771682e+05]
[0.0000000e+00 1.0000000e+00 0.0000000e+00 1.3029813e+05 1.4553006e+05
3.2387668e+05]
[0.0000000e+00 0.0000000e+00 1.0000000e+00 1.2054252e+05 1.4871895e+05
3.1161329e+05]
[1.0000000e+00 0.0000000e+00 0.0000000e+00 1.2333488e+05 1.0867917e+05
3.0498162e+05]]躲避虚拟变量陷阱
在回归预测中我们需要所有的数据都是numeric的,但是会有一些非numeric的数据,比如国家,省,部门,性别。这时候我们需要设置虚拟变量(Dummy variable)。做法是将此变量中的每一个值,衍生成为新的变量,是设为1,否设为0.举个例子,“性别”这个变量,我们可以虚拟出“男”和”女”两虚拟变量,男性的话“男”值为1,”女”值为,;女性的话“男”值为0,”女”值为1。
但是要注意,这时候虚拟变量陷阱就出现了。就拿性别来说,其实一个虚拟变量就够了,比如 1 的时候是“男”, 0 的时候是”非男”,即为女。如果设置两个虚拟变量“男”和“女”,语义上来说没有问题,可以理解,但是在回归预测中会多出一个变量,多出的这个变量将会对回归预测结果产生影响。一般来说,如果虚拟变量要比实际变量的种类少一个。
在多重线性回归中,变量不是越多越好,而是选择适合的变量。这样才会对结果准确预测。如果category类的特征都放进去,拟合的时候,所有权重的计算,都可以有两种方法实现,一种是提高某个category的w,一种是降低其他category的w,这两种效果是等效的,也就是发生了共线性,虚拟变量系数相加和为1,出现完全共线陷阱。
他想表达的是,像“男”“女”这样的数据完全可以用“0”“1”这样一位二进制表示,而看这个数据集只出现了三个州,理论上只用2位二进制(00、01、10)表示就行了,而自动生成的有3位二进制,可能会导致模型不准确。
这里我们用X1验证一下。(后面会发现相差无几,当然人家指明了我们以后注意一下就好)X1 = X[: , 1:]
拆分数据集为训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state = 0)
X1_train, X1_test, Y1_train, Y1_test = train_test_split(X1, Y, test_size = 0.2, random_state = 0)
print(X_test)
print(Y_test)
print(X1_test)
print(Y1_test)[[0.0000000e+00 1.0000000e+00 0.0000000e+00 6.6051520e+04 1.8264556e+05
1.1814820e+05]
[1.0000000e+00 0.0000000e+00 0.0000000e+00 1.0067196e+05 9.1790610e+04
2.4974455e+05]
[0.0000000e+00 1.0000000e+00 0.0000000e+00 1.0191308e+05 1.1059411e+05
2.2916095e+05]
[0.0000000e+00 1.0000000e+00 0.0000000e+00 2.7892920e+04 8.4710770e+04
1.6447071e+05]
[0.0000000e+00 1.0000000e+00 0.0000000e+00 1.5344151e+05 1.0114555e+05
4.0793454e+05]
[0.0000000e+00 0.0000000e+00 1.0000000e+00 7.2107600e+04 1.2786455e+05
3.5318381e+05]
[0.0000000e+00 0.0000000e+00 1.0000000e+00 2.0229590e+04 6.5947930e+04
1.8526510e+05]
[0.0000000e+00 0.0000000e+00 1.0000000e+00 6.1136380e+04 1.5270192e+05
8.8218230e+04]
[0.0000000e+00 1.0000000e+00 0.0000000e+00 7.3994560e+04 1.2278275e+05
3.0331926e+05]
[0.0000000e+00 1.0000000e+00 0.0000000e+00 1.4210734e+05 9.1391770e+04
3.6616842e+05]]
[103282.38 144259.4 146121.95 77798.83 191050.39 105008.31 81229.06
97483.56 110352.25 166187.94]
[[1.0000000e+00 0.0000000e+00 6.6051520e+04 1.8264556e+05 1.1814820e+05]
[0.0000000e+00 0.0000000e+00 1.0067196e+05 9.1790610e+04 2.4974455e+05]
[1.0000000e+00 0.0000000e+00 1.0191308e+05 1.1059411e+05 2.2916095e+05]
[1.0000000e+00 0.0000000e+00 2.7892920e+04 8.4710770e+04 1.6447071e+05]
[1.0000000e+00 0.0000000e+00 1.5344151e+05 1.0114555e+05 4.0793454e+05]
[0.0000000e+00 1.0000000e+00 7.2107600e+04 1.2786455e+05 3.5318381e+05]
[0.0000000e+00 1.0000000e+00 2.0229590e+04 6.5947930e+04 1.8526510e+05]
[0.0000000e+00 1.0000000e+00 6.1136380e+04 1.5270192e+05 8.8218230e+04]
[1.0000000e+00 0.0000000e+00 7.3994560e+04 1.2278275e+05 3.0331926e+05]
[1.0000000e+00 0.0000000e+00 1.4210734e+05 9.1391770e+04 3.6616842e+05]]
[103282.38 144259.4 146121.95 77798.83 191050.39 105008.31 81229.06
97483.56 110352.25 166187.94]第2步:在训练集上训练多元线性回归模型
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, Y_train)
regressor1 = LinearRegression()
regressor1.fit(X1_train, Y1_train)第3步:在测试集上预测结果
y_pred = regressor.predict(X_test)
y1_pred = regressor1.predict(X1_test)
print(y_pred)
print(y1_pred)[103015.20159796 132582.27760815 132447.73845173 71976.09851258
178537.48221051 116161.24230163 67851.69209676 98791.73374689
113969.43533011 167921.06569547]
[103015.20159795 132582.27760817 132447.73845176 71976.09851257
178537.48221058 116161.24230165 67851.69209675 98791.73374686
113969.43533013 167921.06569553]可以发现两组数据相差无几,可能虚拟变量陷阱在这里表现得还不是很明显吧,作者很尴尬咯……
