在结合手写数字识别项目 深入理解多层感知机(Multi-Layer Perceptron)一文中我提及了激活函数以及反向传播算法,但限于篇幅没有具体介绍,特在此开文记录学习过程。
激活函数的特点
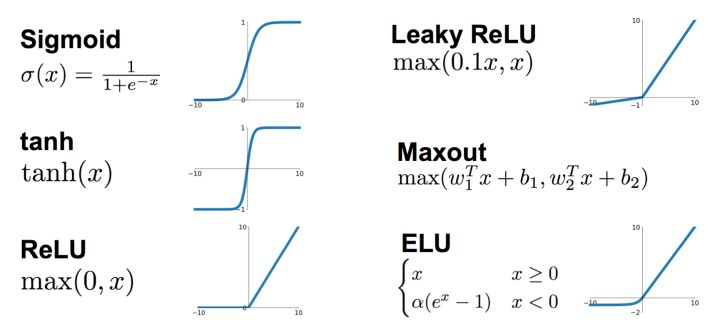
这张图我在前文提及过,其给出了目前常用的一些激活函数。事实上单个感知机也是存在激活函数的: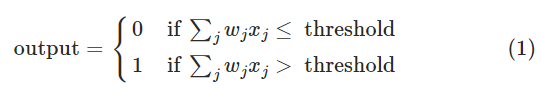
你可能会意外:哈?这种阶跃函数还能叫激活函数?首先,激活函数不是真的要去激活什么。在神经网络中,激活函数的作用是能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题。实际上只要函数具有以下特性,都能被用作激活函数:
- ⾮线性: 即导数不是常数,不然就退化成直线。对于⼀些画⼀条直线仍然⽆法分开的问题,⾮线性可以把直线掰弯,⾃从变弯以后,就能包罗万象了。
- ⼏乎处处可导:也就是具备“丝滑的特性”,不要应激过度,要做正常⼈。数学上,处处可导为后⾯降到的后向传播算法(BP算法)提供了核⼼条件
- 输出范围有限:⼀般是限定在[0,1],有限的输出范围使得神经元对于⼀些⽐较⼤的输⼊也会⽐较稳定。
- ⾮饱和性:饱和就是指,当输⼊⽐较⼤的时候,输出⼏乎没变化了,那么会导致梯度消失!
什么是梯度消失:就是你天天给⼥⽣送花,⼀开始妹纸还惊喜,到后来直接⿇⽊没反应了。梯度消失带来的负⾯影响就是限制了神经⽹络表达能⼒。
sigmod,tanh函数都是软饱和的,阶跃函数是硬饱和,待会详细介绍。
如果激活函数是饱和的,带来的缺陷就是系统迭代更新变慢,系统收敛就慢,当然这是可以有办法弥补的,⼀种⽅法是使⽤交叉熵函数作为损失函数,这⾥不多说。ReLU是⾮饱和的,亲测效果挺不错,所以这货最近挺⽕的。
- 单调性:即导数符号不变。导出要么⼀直⼤于0,要么⼀直⼩于0,不要上蹿下跳。导数符号不变,让神经⽹络训练容易收敛。
这里可能很多人对引入非线性的因素,即第一点不太理解,这里我们拿逻辑回归举个栗子: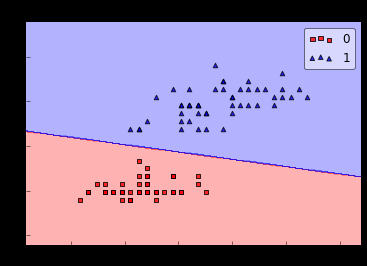
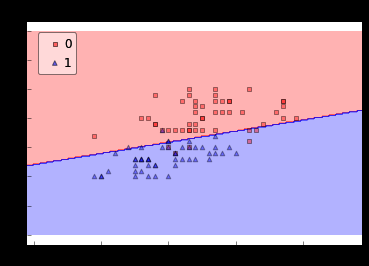
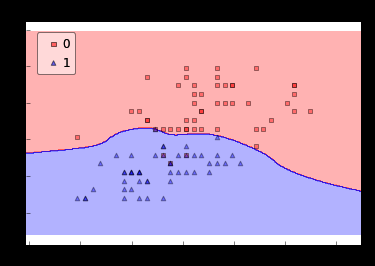
对第一幅图,人也能轻易地画一条直线进行分类;对第二幅图,用直线进行分类已经比较困难了;显然对第二、三幅图用曲线分类是更好的选择,这对神经网络中引入非线性因素给予了很大启发。
激活函数的一些小概念
饱和
当激活函数f(x)满足$ \lim_{x \rightarrow +\infty}f'(x)=0 $时称为激活函数右饱和,同理满足$ \lim_{x \to -\infty}\frac{\mathrm{d} f(x)}{\mathrm{d} x}=0 $称其左饱和,当一个激活函数既左饱和又右饱和时称其饱和。
结合微积分上册知识,饱和之意即为当自变量无穷大时自变量的变化很难引起函数值的变化。
硬饱和与软饱和
对任意的x,如果存在常数c,当x>c时恒有 f′(x)=0则称其为右硬饱和,当x<c时恒有f′(x)=0则称其为左硬饱和。若既满足左硬饱和,又满足右硬饱和,则称这种激活函数为硬饱和。只有在极限状态下偏导数等于0的函数,称之为软饱和。
结合以上两例,我们看到,sigmoid,tanh函数都是软饱和的,阶跃函数是硬饱和的。软是指输⼊趋于⽆穷⼤的时候输出⽆限接近上限,硬是指像阶跃函数那样,输⼊⾮0输出就已经始终都是上限值。
饱和会给训练神经网络带来一些问题,例如我在MNIST手写数字识别中出现的增加隐藏层的个数识别准确率反而降低的问题,这涉及到梯度消失与梯度爆炸,争取年后开文介绍。
激活函数的选取
尽管学者们已经在激活函数上花了大量的功夫研究,但激活函数的选取目前不存在定论。对初学者而言对每个激活函数都尝试一下,或许会得到意想不到的发现。事实上,在实际工作中,不同的项目和应用,激活函数的不同往往会给项目开发带来不一样的姿色。
准备工作
回顾一下复合函数求导法则,尝试对Sigmoid函数求导。
$ y'=(\frac{1}{e^{-x}+1})'=y\cdot (1-y) $自己算,别偷懒,加深理解。导数图像:
Sigmoid函数求导十分方便是其在初期被选为激活函数的重要原因,毕竟谁不想多省点电为环保做贡献呢?
概念
正向传播:按照目前的权重与偏置根据第一层的输入逐层下放,求出各层激活值。
反向传播:根据结果与期望的差距调整权重与偏置,反向传播是计算多元函数梯度的重要方法。
推导
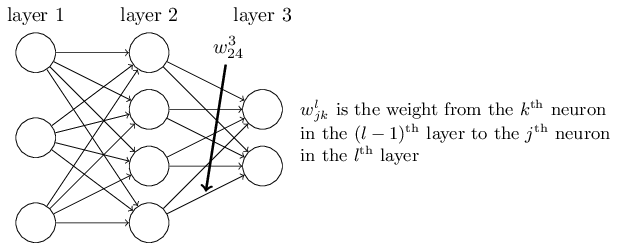
这里w下标的顺序有些奇怪,其实是为后面的式子矩阵化做准备。
$ a^{l}_j = \sigma\left( \sum_k w^{l}_{jk} a^{l-1}_k + b^l_j \right), $ 这个公式描述了每一层各个神经元的激活值计算方法,用向量方法表示:$ a^{l} = \sigma(w^l a^{l-1}+b^l) $
对向量取Sigmoid时是对其的所有元素分别取Sigmoid。运算法则像这样:
再作两个假设:
- 代价函数能被写作单样本损失函数的平均值,即$ C = \frac{1}{n} \sum_x C_x $,显然我们的LMS最小均方代价函数满足这个要求。
Why:反向传播实际上做的就是在单个训练样本上计算$ \frac{\partial C}{\partial w^l_jk} $ ,然后通过平均所有样本计算$ \frac{\partial C}{\partial w} $ $ \frac{\partial C}{\partial b} $。 - 代价函数能被写作含有神经网络输出的函数。如: $ C(x) = \frac{1}{2} \|y-a^L\|^2 = \frac{1}{2} \sum_j (y_j-a^L_j)^2 $
需要注意的是:这个函数看上去以y作为自变量。但其实只要输入的训练样本x一确定,y也随之确定。
反向传播背后的四个基本公式

BP1式
$$\delta^L = (a^L-y) \odot \sigma'(z^L)$$
引入中间变量$ \delta^l_j $,称为第l层第j个神经元的Error。反向传播将会给出计算Error的具体方法,并将其与$ \frac{\partial C}{\partial w^l_jk} $和 $ \frac{\partial C}{\partial b^l_j} $挂钩。
假设有一个恶魔坐在第l层的第j个神经元上,恶魔会对输入神经元的数据(加权后)做手脚使其变化$ \Delta z^l_j $,这个神经元将不再输出$ \sigma(z^l_j) $,而是输出$ \sigma(z^l_j+\Delta z^l_j) $ ,这导致了总的代价函数变化了$ \frac{\partial C}{\partial z^l_j} \cdot \Delta z^l_j $。
现在,这只恶魔是一只好恶魔,他像你一样也希望代价函数的值变小,也就是说他想找到一个$ \Delta z^l_j $使得代价函数变小。
我们定义$ \delta^l_j $为
$$ \delta^l_j \equiv \frac{\partial C}{\partial z^l_j} $$
像之前那样,我们用$ \delta^l $表示第l层所有神经元的Error。其中每一个元素由$$ \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j)$$ 给出。(BP1式的分量形式)
证明:由链式法则将上面的偏导形式写成$\delta^L_j = \sum_k \frac{\partial C}{\partial a^L_k} \frac{\partial a^L_k}{\partial z^L_j}$,显然$k\neq j$时$\partial a^L_k / \partial z^L_j = 0$,所以上式化简为$ \delta^L_j = \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_j} $ ,又因为$ a^L_j = \sigma(z^L_j) $所以等式右边第二项可写作$ \sigma'(z^L_j) $,所以原式$\delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j)$成立。
BP1式中的每一项都很好计算:这里需要指出的是对$ \partial C / \partial a^L_j $,由于形式特殊的激活函数 $C = frac{1}{2} sum_j
(y_j-a^L_j)^2 $,偏导$ frac{partial C}{partial a^L_j} = (a_j^L-y_j) $ 也很好计算。
BP1式写作向量形式表示为$$\delta^L = \nabla_a C \odot \sigma'(z^L)$$,在此题背景下可以简化为$\delta^L = (a^L-y) \odot \sigma'(z^L)$
$$\delta^l = \Sigma'(z^l) (w^{l+1})^T \delta^{l+1} $$
$$ \delta^l = \Sigma'(z^l) (w^{l+1})^T \ldots \Sigma'(z^{L-1}) (w^L)^T \Sigma'(z^L) \nabla_a C $$
显然传统矩阵乘法的形式可能对某些人更容易理解。
BP2式
$$ \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) $$
结合BP1式与BP2式我们可以计算网络中任意一层的$\delta^l$。
BP3式
$$ \frac{\partial C}{\partial b^l_j} = \delta^l_j $$
BP3式表明:$ \delta^l_j $恰好等于$\partial C / \partial b^l_j$,这可是个大好消息,因为通过BP1、BP2两式正好可以计算出$\partial C / \partial b^l_j$。
BP3式用于计算网络中任意一个偏置的变化率。
BP4式
$$\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j $$
如果去掉角标更容易理解的话可以看$$\frac{\partial C}{\partial w} = a_{\rm in} \delta_{\rm out}$$
用图片可以简化为: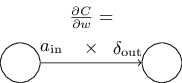
我们会会发现,如果输入激活值很小,例如趋近于0,那么$ \partial C / \partial w $也会很小,这时我们就说学习缓慢,因为权重值在梯度下降过程中变化不明显。
其实仔细观察上面四个式子还能得到一些其他结论:
- 当$ z^L_j$ 趋近于正(负)无穷时,$\sigma'(z^L_j) \approx 0$ ,此时从BP1式我们得知学习也变得缓慢了,这是我们称输出神经元“饱和”(saturated),同样的情况在计算偏置时也会出现。
